Demystifying the Karnaugh Map: A Comprehensive Guide to Three-Variable Logic Minimization
Related Articles: Demystifying the Karnaugh Map: A Comprehensive Guide to Three-Variable Logic Minimization
Introduction
With enthusiasm, let’s navigate through the intriguing topic related to Demystifying the Karnaugh Map: A Comprehensive Guide to Three-Variable Logic Minimization. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
- 1 Related Articles: Demystifying the Karnaugh Map: A Comprehensive Guide to Three-Variable Logic Minimization
- 2 Introduction
- 3 Demystifying the Karnaugh Map: A Comprehensive Guide to Three-Variable Logic Minimization
- 3.1 Constructing a Three-Variable Karnaugh Map
- 3.2 Simplifying Boolean Expressions using K-maps
- 3.3 Benefits of Using Karnaugh Maps
- 3.4 FAQs about Three-Variable Karnaugh Maps
- 3.5 Tips for Using Karnaugh Maps Effectively
- 3.6 Conclusion
- 4 Closure
Demystifying the Karnaugh Map: A Comprehensive Guide to Three-Variable Logic Minimization
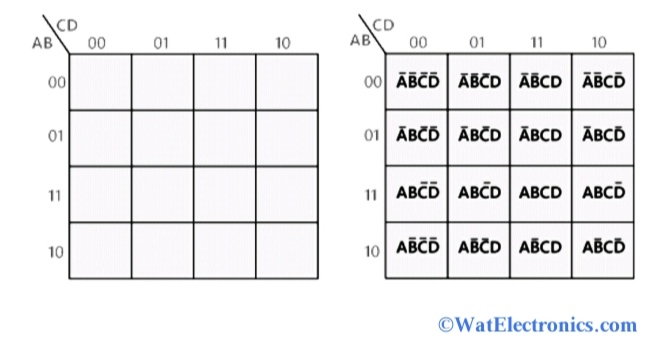
The Karnaugh Map, often abbreviated as K-map, is a visual tool used in digital logic design for simplifying Boolean expressions. It provides a graphical representation of a truth table, facilitating the identification of groups of minterms (or maxterms) that can be combined to reduce the complexity of a logic circuit. This simplification leads to more efficient and cost-effective designs, particularly relevant in the context of minimizing the number of logic gates required to implement a given function.
While K-maps can be applied to functions with any number of variables, their effectiveness is most pronounced for functions with up to four variables. This article focuses on the application of K-maps to three-variable logic functions, providing a detailed understanding of their construction, interpretation, and application in simplifying Boolean expressions.
Constructing a Three-Variable Karnaugh Map
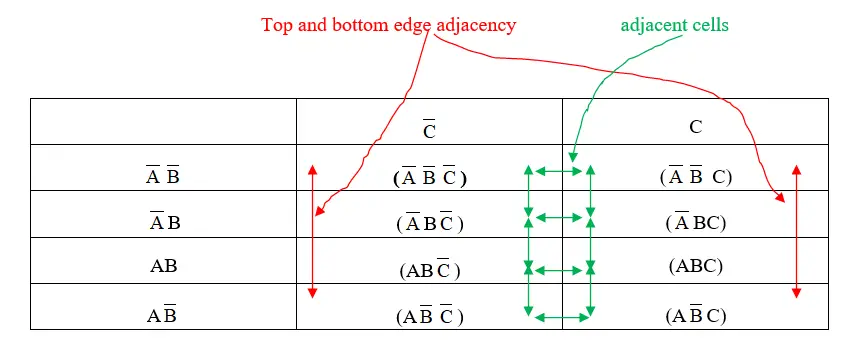
A three-variable K-map consists of a 2×4 grid, with each cell representing a unique combination of the three input variables. The rows and columns are labeled according to a specific binary code that ensures adjacent cells differ by only one bit. This arrangement is crucial for identifying groups of minterms that can be combined for simplification.
The Standard Labeling Convention:
- Rows: The two rows are labeled with the binary combinations of the two variables that change the least frequently, typically the least significant bits (LSB).
- Columns: The four columns are labeled with the binary combinations of the remaining variable, which changes more frequently, typically the most significant bit (MSB).
Example:
Consider a function with input variables A, B, and C. The K-map would be labeled as follows:
| ABC | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | ||||
| 01 |
Filling the K-map:
Each cell in the K-map corresponds to a unique combination of the input variables. The cell is marked with a ‘1’ if the function evaluates to ‘1’ for that particular input combination, and with a ‘0’ otherwise. This process essentially transforms the truth table into a visual representation.
Example:
Let’s say we have a function defined by the following truth table:
| A | B | C | F(A,B,C) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
The corresponding K-map would look like this:
| ABC | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 0 | 1 | 0 | 1 |
| 01 | 1 | 0 | 1 | 1 |
Simplifying Boolean Expressions using K-maps
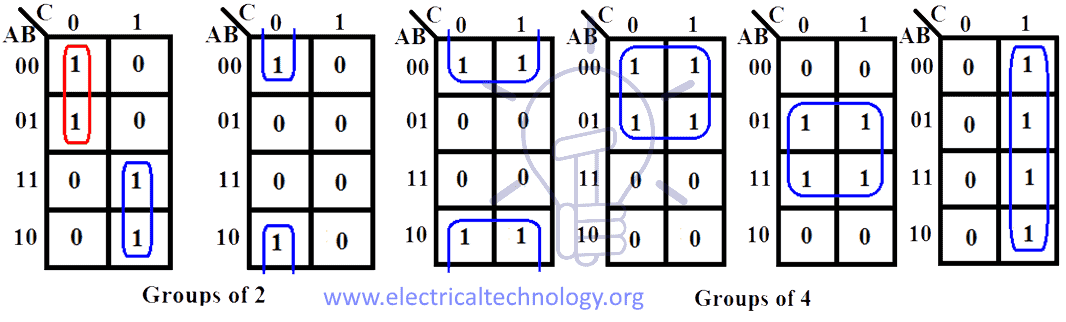
The primary purpose of the K-map is to simplify Boolean expressions by identifying groups of adjacent ‘1’ cells. These groups, known as implicants, represent terms in the simplified expression. The larger the group, the fewer literals (variables) are required in the corresponding term.
Rules for Forming Implicants:
- Adjacency: Cells are considered adjacent if they share a common edge. This includes wrapping around the edges of the map (e.g., the top row is adjacent to the bottom row).
- Size: Implicants can be of any size, as long as they consist of adjacent ‘1’ cells.
- Maximality: It’s advantageous to form the largest possible implicants, as they lead to simpler terms in the simplified expression.
- Overlapping: Implicants can overlap, and a ‘1’ cell can belong to multiple implicants.
Example:
Consider the K-map from the previous example. We can identify the following implicants:
- Group 1: A ‘1’ cell in the top left corner. This represents the term A’B’C.
- Group 2: Two adjacent ‘1’ cells in the top row. This represents the term A’C.
- Group 3: Two adjacent ‘1’ cells in the second row. This represents the term BC.
- Group 4: Two adjacent ‘1’ cells in the rightmost column. This represents the term B.
Simplified Expression:
The simplified Boolean expression for the function is obtained by combining these implicants:
F(A,B,C) = A’B’C + A’C + BC + B
Benefits of Using Karnaugh Maps
- Visual Simplification: K-maps provide a visual representation of the logic function, making it easier to identify and combine terms for simplification.
- Systematic Approach: The grid-based structure and adjacency rules ensure a systematic approach to simplification, reducing the chances of errors.
- Minimization of Logic Gates: Simplified expressions lead to fewer logic gates required to implement the function, resulting in more efficient and cost-effective circuits.
- Easy to Understand and Use: K-maps are relatively easy to learn and use, even for beginners in digital logic design.
FAQs about Three-Variable Karnaugh Maps
Q: How do I determine the order of the variables when labeling the K-map?
A: While the order of variables is not strictly fixed, it’s generally recommended to arrange the variables in descending order of significance, with the most significant bit (MSB) changing most frequently and the least significant bit (LSB) changing least frequently. This helps maintain the adjacency property of the map.
Q: What happens if there are ‘don’t care’ conditions in the truth table?
A: ‘Don’t care’ conditions, represented by an ‘X’ in the truth table and K-map, indicate that the output value doesn’t matter for that particular input combination. These ‘X’ cells can be used to expand existing implicants, leading to further simplification of the expression.
Q: Can I use a K-map to simplify functions with more than three variables?
A: While K-maps can be used for functions with up to four variables, they become increasingly complex and less practical for functions with more variables. For functions with more than four variables, alternative methods like Quine-McCluskey algorithm are preferred.
Tips for Using Karnaugh Maps Effectively
- Practice: The best way to master K-maps is to practice with numerous examples. Start with simple functions and gradually increase the complexity.
- Identify the Largest Implicants: Always aim to form the largest possible implicants, as they will lead to the simplest terms in the simplified expression.
- Use ‘Don’t Care’ Conditions Strategically: Exploit ‘don’t care’ conditions to expand existing implicants and achieve further simplification.
- Verify Your Solution: After obtaining a simplified expression, verify its correctness by comparing it to the original truth table or by simulating the circuit.
Conclusion
The Karnaugh Map is a powerful tool for simplifying Boolean expressions, particularly for functions with up to four variables. Its visual representation and systematic approach make it an effective method for minimizing the complexity of logic circuits. By understanding the principles of K-map construction, interpretation, and simplification, designers can create more efficient, cost-effective, and reliable digital systems. While the advent of automated tools has simplified the process, a thorough understanding of K-maps remains valuable for gaining a deeper insight into the underlying principles of digital logic design and for developing a strong foundation for tackling more complex problems.





Closure
Thus, we hope this article has provided valuable insights into Demystifying the Karnaugh Map: A Comprehensive Guide to Three-Variable Logic Minimization. We thank you for taking the time to read this article. See you in our next article!